I wanted to make this tutorial as beginner friendly as possible.If you didn't understand something, feel free to ask me in the comments, I will reply.I will use c and c++ for this tutorial as it gives much more access and you actually know what you are doing.So I expect you to know the basics of this languages respectively.I wrote a blog of C you can read that.
Let's clear up our basics with these terms before deep diving into DSA. Data Structures and Algorithms are two different things.

Data Structures – These are like the ingredients you need to build efficient algorithms. These are the ways to arrange data so that they (data items) can be used efficiently in the main memory. Ex: Array, Stack, Linked List, and many more.
Algorithms – Sequence of steps performed on the data using efficient data structures to solve a given problem, be it a basic or real-life-based one.Ex: sorting an array.

Some other Important terminologies:
Database – Collection of information in permanent storage for faster retrieval and updation. Examples: MySql, MongoDB, etc.
Data warehouse – Management of huge data of legacy data( the data we keep at a different place from our fresh data in the database to make the process of retrieval and updation fast) for better analysis.
Big data – Analysis of too large or complex data, which cannot be dealt with the traditional data processing applications.

Memory Layout of C Programs:
When the program starts, its code gets copied to the main memory.
The stack holds the memory occupied by functions. It stores the activation records of the functions used in the program. And erases them as they get executed.
The heap contains the data which is requested by the program as dynamic memory using pointers.
Initialized and uninitialized data segments hold initialized and uninitialized global variables, respectively.

A few algorithm examples:

BIG O notation

Big O notation is used in Computer Science to describe the performance or complexity of an algorithm. Big O specifically describes the worst-case scenario, and can be used to describe the execution time required or the space used (e.g. in memory or on disk) by an algorithm.

O(1)

void printFirstElementOfArray(int arr[])
{
    printf("First element of array = %d",arr[0]);
}

This function runs in O(1) time (or "constant time") relative to its input. The input array could be 1 item or 1,000 items, but this function would still just require one step.

O(n)

void printAllElementOfArray(int arr[], int size)
{
    for (int i = 0; i < size; i++)
    {
        printf("%d\n", arr[i]);
    }
}

This function runs in O(n) time (or "linear time"), where n is the number of items in the array. If the array has 10 items, we have to print 10 times. If it has 1000 items, we have to print 1000 times.

O(n2)

void printAllPossibleOrderedPairs(int arr[], int size)
{
    for (int i = 0; i < size; i++)
    {
        for (int j = 0; j < size; j++)
        {
            printf("%d = %d\n", arr[i], arr[j]);
        }
     }
}

Here we're nesting two loops. If our array has n items, our outer loop runs n times and our inner loop runs n times for each iteration of the outer loop, giving us n2 total prints. Thus this function runs in O(n2) time (or "quadratic time"). If the array has 10 items, we have to print 100 times. If it has 1000 items, we have to print 1000000 times.

Data Structure

Linked Lists:
A linked list is a linear data structure that includes a series of connected nodes. Here, each node stores the data and the address of the next node. For example,

You have to start somewhere, so we give the address of the first node a special name called HEAD. Also, the last node in the linked list can be identified because its next portion points to NULL.

Linked lists can be of multiple types: singly, doubly, and circular linked list. In this article, we will focus on the singly linked list.

Representation of Linked List
Let's see how each node of the linked list is represented. Each node consists:

A data item
An address of another node
We wrap both the data item and the next node reference in a struct as:

struct node
{
  int data;
  struct node *next;
};

Each struct node has a data item and a pointer to another struct node. Let us create a simple Linked List with three items to understand how this works.

/* Initialize nodes */
struct node *head;
struct node *one = NULL;
struct node *two = NULL;
struct node *three = NULL;

/* Allocate memory */
one = malloc(sizeof(struct node));
two = malloc(sizeof(struct node));
three = malloc(sizeof(struct node));

/* Assign data values */
one->data = 1;
two->data = 2;
three->data=3;

/* Connect nodes */
one->next = two;
two->next = three;
three->next = NULL;

/* Save address of first node in head */
head = one;

The power of a linked list comes from the ability to break the chain and rejoin it. E.g. if you wanted to put an element 4 between 1 and 2, the steps would be:

-Create a new struct node and allocate memory to it.
-Add its data value as 4
-Point its next pointer to the struct node containing 2 as the data value
-Change the next pointer of "1" to the node we just created.
-Doing something similar in an array would have required
-shifting the positions of all the subsequent elements.

Binary Search Tree:

Binary search tree is a data structure that quickly allows us to maintain a sorted list of numbers.

It is called a binary tree because each tree node has a maximum of two children.
It is called a search tree because it can be used to search for the presence of a number in O(log(n)) time.
The properties that separate a binary search tree from a regular binary tree is

All nodes of left subtree are less than the root node
All nodes of right subtree are more than the root node
Both subtrees of each node are also BSTs i.e. they have the above two properties.

The binary tree on the right isn't a binary search tree because the right subtree of the node "3" contains a value smaller than it.

Searching a key
For searching a value, if we had a sorted array we could have performed a binary search. Let’s say we want to search a number in the array, in binary search, we first define the complete list as our search space, the number can exist only within the search space. Now we compare the number to be searched or the element to be searched with the middle element (median) of the search space and if the record being searched is less than the middle element, we go searching in the left half, else we go searching in the right half, in case of equality we have found the element. In binary search we start with ‘n’ elements in search space and if the mid element is not the element that we are looking for, we reduce the search space to ‘n/2’ we keep reducing the search space until we either find the record that we are looking for or we get to only one element in search space and be done with this whole reduction.

// C function to search a given key in a given BST
struct node* search(struct node* root, int key)
{
    // Base Cases: root is null or key is present at root
    if (root == NULL || root->key == key)
    return root;

    // Key is greater than root's key
    if (root->key < key)
    return search(root->right, key);

    // Key is smaller than root's key
    return search(root->left, key);
}

Illustration to search 6 in below tree:

Start from the root.
Compare the searching element with root, if less than root, then recursively call left subtree, else recursively call right subtree.
If the element to search is found anywhere, return true, else return false.

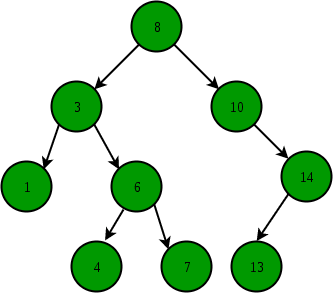
Insertion of a key
A new key is always inserted at the leaf. We start searching a key from the root until we hit a leaf node. Once a leaf node is found, the new node is added as a child of the leaf node.

// C++ program to demonstrate insertion
// in a BST recursively.
#include <iostream>
using namespace std;

class BST {
    int data;
    BST *left, *right;

public:
    // Default constructor.
    BST();

    // Parameterized constructor.
    BST(int);

    // Insert function.
    BST* Insert(BST*, int);

    // Inorder traversal.
    void Inorder(BST*);
};

// Default Constructor definition.
BST ::BST()
    : data(0)
    , left(NULL)
    , right(NULL)
{
}

// Parameterized Constructor definition.
BST ::BST(int value)
{
    data = value;
    left = right = NULL;
}

// Insert function definition.
BST* BST ::Insert(BST* root, int value)
{
    if (!root) {
        // Insert the first node, if root is NULL.
        return new BST(value);
    }

    // Insert data.
    if (value > root->data) {
        // Insert right node data, if the 'value'
        // to be inserted is greater than 'root' node data.

        // Process right nodes.
        root->right = Insert(root->right, value);
    }
    else {
        // Insert left node data, if the 'value'
        // to be inserted is greater than 'root' node data.

        // Process left nodes.
        root->left = Insert(root->left, value);
    }

    // Return 'root' node, after insertion.
    return root;
}

// Inorder traversal function.
// This gives data in sorted order.
void BST ::Inorder(BST* root)
{
    if (!root) {
        return;
    }
    Inorder(root->left);
    cout << root->data << endl;
    Inorder(root->right);
}

// Driver code
int main()
{
    BST b, *root = NULL;
    root = b.Insert(root, 50);
    b.Insert(root, 30);
    b.Insert(root, 20);
    b.Insert(root, 40);
    b.Insert(root, 70);
    b.Insert(root, 60);
    b.Insert(root, 80);

    b.Inorder(root);
    return 0;
}

Output:
20
30
40
50
60
70
80

Arrays:

An array in C/C++ or be it in any programming language is a collection of similar data items stored at contiguous memory locations and elements can be accessed randomly using indices of an array. They can be used to store collection of primitive data types such as int, float, double, char, etc of any particular type. To add to it, an array in C/C++ can store derived data types such as the structures, pointers etc. Given below is the picture representation of an array.

There are various ways in which we can declare an array. It can be done by specifying its type and size, by initializing it or both.

Array declaration by specifying size

//C code below
// Array declaration by specifying size
int arr1[10];

// With recent C/C++ versions, we can also
// declare an array of user specified size
int n = 10;
int arr2[n];

// Array declaration by initializing elements
int arr[] = { 10, 20, 30, 40 }

// Compiler creates an array of size 4.
// above is same as "int arr[4] = {10, 20, 30, 40}"

Array declaration by specifying size and initializing elements

// Array declaration by specifying size and initializing
// elements
int arr[6] = { 10, 20, 30, 40 }

// Compiler creates an array of size 6, initializes first
// 4 elements as specified by user and rest two elements as
// 0. above is same as "int arr[] = {10, 20, 30, 40, 0, 0}"

Advantages of an Array in C/C++:

-Random access of elements using array index.
-Use of fewer line of code as it creates a single array of multiple elements.
-Easy access to all the elements.
-Traversal through the array becomes easy using a single loop.
-Sorting becomes easy as it can be accomplished by writing fewer line of code.

///////////////////////////////////////

Buy me a coffee
Thanks for reading!
Hope you learnt something new today
Cheers!

Introduction to Data structures and algorithms

BIG O notation

Data Structure

Arrays: