Binary Search Trees (BSTs) have always been one of those things that seems to leave my knowledge as soon as I try and commit any possible method or structure for it to memory, hence why I'm writing this article! I'll be going over some different strategies and approaches that'll hopefully save you from that same fate I've experienced time and time again

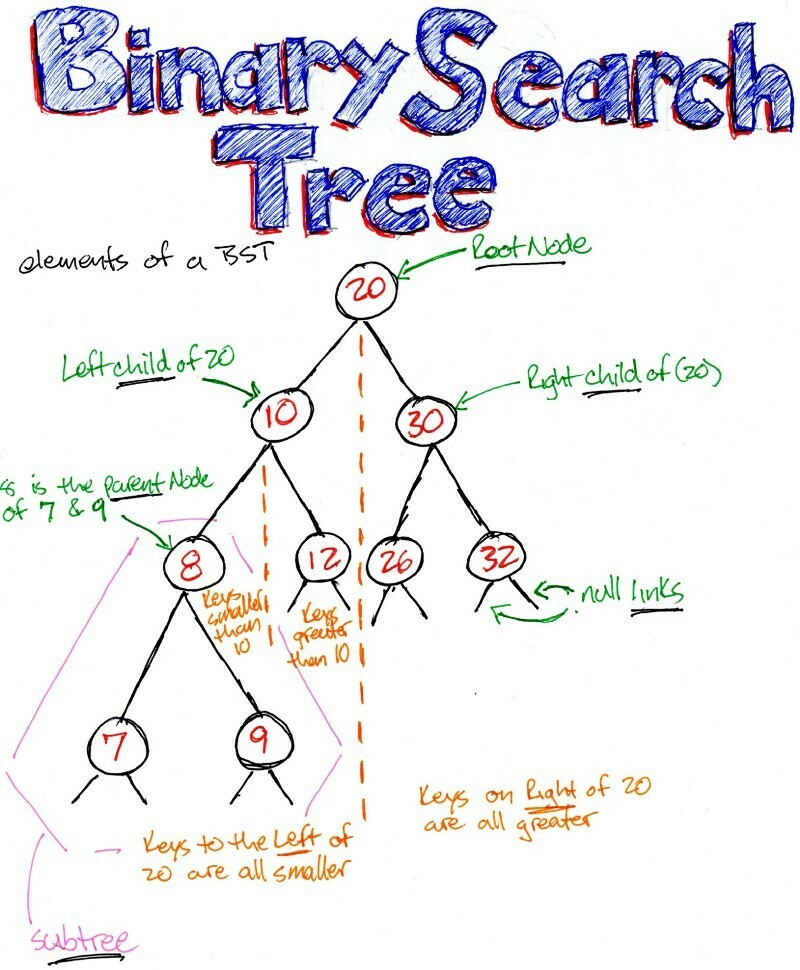
Before we dive into the code, let's first talk about the general structure of a BST with the help of this handy graphic made by the wonderful Kevin Turney in conjunction with freeCodeCamp:

For those who didn't study that graphic for too long (raises hand guiltily), basically all it's saying is that you start with a root node that will be the starting point for all further nodes to be placed into. Think of it like the root of a tree, which is where the source of the tree's existence is managed (see what they did there when they thought to name this concept after a tree?)

The next major point in the graphic is that all nodes will have a left and a right node that its associated with. If no value is defined for either the left or the right node, it's default value will be null. Think of nodes as simply the next value tied to another node that will have an additional two properties on it (typically labeled left and right) that will accommodate the insertion of even MORE nodes

Also, the overarching theme for BST's is that if a node's value is less than the root's, it will go to the left of the root. Similarly, if a node's value is greater than the root's, it will go to the right of the root

So once again, if it's less than the root, to the left it goes; if it's greater than the root, to the right it goes!

Good. Now we've firmly solidified that concept in our brains. Awesome job, you're doing great! (seriously)

So now that we've gotten the formalities and "theory" (blech) out of the way, let's start diving into some actual code! The first piece I'd like to start with is simply creating the structure in which our nodes can be formed. You can also refer to nodes as leaves (that's the joke I was aiming for when I titled this article.........LAUGH DANG IT)

Alright, so with that, let's check out our baseline approach using ES6+ classes in JavaScript:

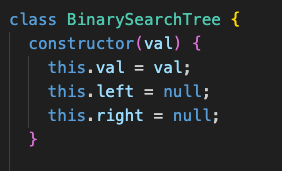
We have our class labeled BinarySearchTree and it contains a constructor with a few properties within it:

• this.val (value)
• this.left
• this.right

This is what we've already discussed in the graphic from earlier; if no root is established when we first create our BST, this.val will automatically become the root. Henceforth, that root will have two additional properties on it which will accommodate additional nodes (or leaves, heh).

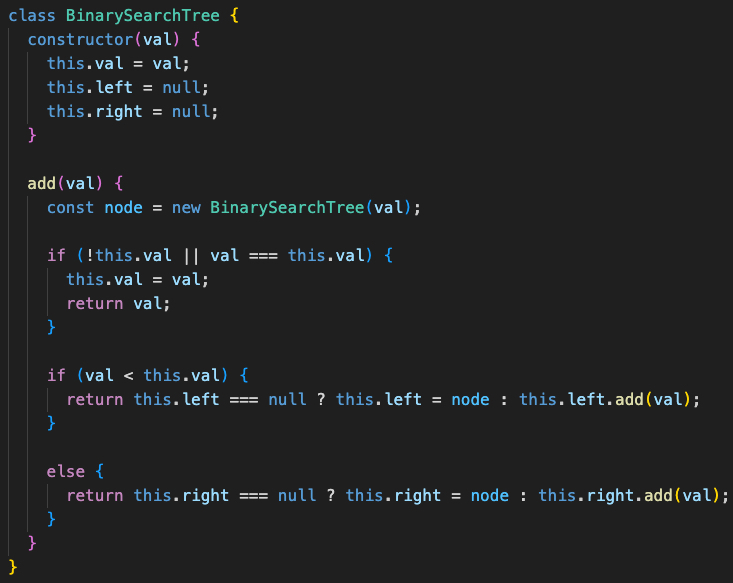
So that's great 'n all, but what do we do after we've already established the root and wish to adhere to the BST principle of populating our tree with additional nodes that differ in value from our root? Enter the add() method:

Alright, don't click off the page, please! I know it's a lot. Trust me, I know. There's a lot happening here. Let's break this down together.

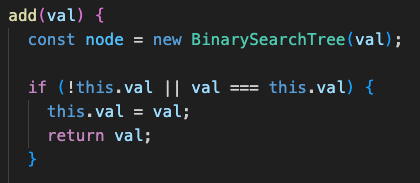
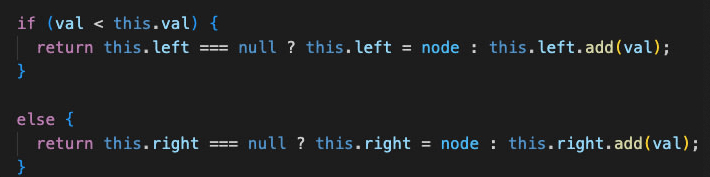
Let's first focus on this part:

Essentially all that's happening is we're declaring an add() method in our BinarySearchTree class that'll take in whatever value (val) we provide to it and then perform some action on that value. The first thing we do inside of the add method is declare a constant that's assigned to a new instance of the BinarySearchTree class with the passed in parameter of val

We then check if the current property this.val has anything assigned to it OR if the value for it is equivalent to the value that has been passed in. This is a duality check in seeing if a meaningful value (i.e., not null) has been assigned to the current node or if the value being passed already exists within the tree.

For the vast majority of BST's, it's generally recognized that duplicate values won't be utilized, hence the statement after the || (logical OR) operator. So any values that already exist, we don't give a damn about and will want to reassign!

Cool, so we've established what's happening with our first variable declaration and our first conditional statement. Now let's dive into the next section of our add() method:

Ternary Operator Heaven

If you're not familiar with ternary operators, I don't blame you. They're confusing as heck the first time you come across them. The mnemonic that helped me to understand this conditional operator is whatever comes prior to the : will be true. If it's not true, then whatever is after the : will be accepted if the condition evaluates to false. The mnemonic being "Is it true? That first thing. It's not true? That second thing".

Alright, so with that, let's explore what these two conditional statements are doing; the first if statement is checking to see if the passed in value is less than the current node's value. If it is, then we'll enter into this statment. One of two things will happen once we enter, based off this condition:

Does a value exist (not null) to the left of the current node?

1.) If not, assign this.left to the passed in node
2.) If yes, recursively enter a new execution context

And it's pretty much the same concept for this other piece of code:

If the passed in value is greater than the current node's value, we'll enter into it. Then we repeat that very same logic we've already discussed.

And that's basically it for establishing a binary search tree and implementing an add method into it that will forgo duplicate values! Ternary operations really help me with memorizing complex data structure solutions and I hope this approach gives you some value too!

I have a few other methods that utilize ternary operations for includes(), min() and max() methods. If you'd like me to elaborate more on those and even more additional BST methods, please let me know!

Thank you for reading this far and I'd be honored if you gave me a follow and a reaction if you found any value from this post!

<3<3<3