Welcome back to my series of Advent of Code solutions in MiniScript! In Day 17 we got to (sort of) play Tetris. Five different Tetris-like shapes fall into a pit, moved left or right on each step according to the input. The first task is to see how high this stack will grow after 2022 blocks have been dropped in.
(Dev.to doesn't allow right-aligned images, so I've rotated the visualization above. Please turn your monitor sideways for proper viewing.)
To solve this, I approached it much like making a video game. The blocks in the challenge description are referred to as "rocks with peculiar shapes," so I made a Rock class that represents one such rock. The exact shape is defined by a pattern list that has one string per row, just like in the challenge. The Rock class has methods to check whether it would hit something (the an already-placed Rock, or the edge of the pit) at a given x,y position; and to "settle" (that is, add itself permanently to the pit).
The pit itself is represented as a list of lists called column. column[n] represents the nth column, as a list of 1-character strings, either "." for empty, or "#" for a settled rock.
To drop a rock into the pit, the add1rock method first figures the proper starting position according to the rules, then repeatedly applies "gas" (a left or right nudge according to the input) and moves the block down 1 row, until it can't move down any more. Then it settles the rock and returns.
Finally, the main loop is trivial: it just calls add1Rock the required number of times, cycling through the five different rock shapes. At the end, we report how big the column lists got, which we kept track of in colHeight
if 1 then fname = "input.txt" else fname = "example.txt"
gas = file.readLines(fname)[0]
nextGasNum = 0
column = [[]] * 7 // contents of each column of the pit
colHeight = 0 // height (always equal to column[n].len)
// Rock class: represents a Tetris-like block dropped in
Rock = {}
Rock.pattern = []
Rock.make = function(pattern)
noob = new Rock
noob.pattern = pattern
noob.width = pattern[0].len
noob.height = pattern.len
return noob
end function
Rock.hitsSomethingAt = function(x,y)
if x + self.width > 7 then return true
if x < 0 then return true
if y < 0 then return true
for row in self.pattern.indexes
if y + row >= colHeight then return false
p = self.pattern[self.height - 1 - row]
for col in p.indexes
if p[col] != "#" then continue
if column[x + col][y + row] == "#" then return true
end for
end for
return false
end function
Rock.settle = function(x, y)
// first, grow all columns as needed
newHeight = y + self.height
if colHeight < newHeight then
for col in column.indexes
column[col] = column[col] + ["."] * (newHeight-colHeight)
end for
globals.colHeight = newHeight
end if
// then stuff the rock into the columns
for row in self.pattern.indexes
p = self.pattern[self.height - 1 - row]
for col in p.indexes
if p[col] != "#" then continue
column[x + col][y + row] = "#"
end for
end for
end function
rock0 = Rock.make(["####"])
rock1 = Rock.make([".#.", "###", ".#."])
rock2 = Rock.make(["..#", "..#", "###"])
rock3 = Rock.make(["#"]*4)
rock4 = Rock.make(["##", "##"])
rocks = [rock0, rock1, rock2, rock3, rock4]
add1Rock = function(rock)
// left edge 2 units away from left wall
x = 2
// bottom edge 3 units above highest rock (or floor)
y = colHeight + 3
while true
// apply gas
dir = gas[nextGasNum]
globals.nextGasNum = (nextGasNum + 1) % gas.len
if dir == ">" then
if not rock.hitsSomethingAt(x + 1, y) then
x = x + 1
end if
else
if not rock.hitsSomethingAt(x - 1, y) then
x = x - 1
end if
end if
// fall down
if rock.hitsSomethingAt(x, y - 1) then
// Settled!
rock.settle x, y
return
end if
y = y - 1
end while
end function
nextRockNum = 0
for i in range(1,2022)
add1Rock rocks[nextRockNum]
nextRockNum = (nextRockNum + 1) % rocks.len
end for
print colHeight
For my input file, this took a second or two to compute, and came out to a height of 3173 rows.
Part Two
The second part of the challenge "simply" changes how many blocks we need to drop. Now we have to drop 1 trillion.
I quickly measured how long it took to drop 10,000 blocks, did a little math. At that rate, doing a trillion blocks would take 13.7 years. I didn't think that would get me a good spot in the competition. Obviously some clever trick was needed.
I started by adding the ability to "scroll" the pit, i.e., chop off the bottom so-many rows which are no longer relevant. This changed the portion of Rock.settle than grows the pit as needed:
if colHeight < newHeight then
for col in column.indexes
column[col] = column[col] + ["."] * (newHeight-colHeight)
end for
globals.colHeight = newHeight
if column[0].len > 200 then
globals.colScroll = colScroll + 100
for col in column.indexes
column[col] = column[col][100:]
end for
end if
end if
So, if the columns are bigger than 200 items long, we chop off the first 100, and add 100 to the colScroll amount (which we then use to convert from row numbers to column indexes whenever we inspect or update the contents of the pit).
This solves the memory problem, but still doesn't help us drop a trillion blocks in less than 13 years.
It soon became clear that we would need to find repeating cycles. At this point, I wasted a good 20 or 30 minutes doubting myself, and looking for a cleverer trick. I thought that with my input file (remember, these are the left/right nudges) size of 10091 commands, and 5 different blocks, cycles would have to be some multiple of 50455 iterations long, which seemed excessive. (This was incorrect — I'd forgotten that on each iteration we go through quite a lot of input-file commands, depending on how far the block drops before it settles.)
Finally I coded it up anyway and hoped for the best. But how to detect a cycle? We know it's going to repeat when the current state and some previous step in the simulation exactly match in (1) which step of the input file we're on, (2) which rock we're dropping and, and (3) the top portion of the pit. It's not clear exactly how big this "top portion" has to be; if some pathological point in the input had a few thousand "left" to push all the blocks to the left, leaving a big gap on the right, then we would need to consider a portion thousands of rows high. But the input file looked fairly random, so I suspected we would never need to check that much. I chose to check the top 32 rows, and hope that would be good enough. (Spoiler: it was.)
So, I created a "memo" map to keep track of states we've previously seen, along with the iteration and total height at that point. (This is quite similar to the dynamic programming we did yesterday!) This changed only the main program, which now looks like this:
memo = {} // key: state key; value: [i, colHeight]
nextRockNum = 0
i = 0
while i < 1E12
if colHeight > 32 and memo != null then
keyParts = [nextRockNum, nextGasNum]
for col in column.indexes
keyParts.push column[col][-32:]
end for
key = keyParts.join("")
if memo.hasIndex(key) then
print "HEY!!! Found a cycle at i=" + i + " (colHeight=" + colHeight + ")"
print memo[key]
// Now we have a cycle, we can fast-forward to near a trillion.
lastI = memo[key][0]
lastHeight = memo[key][1]
cycleHeight = colHeight - lastHeight
cycleIters = i - lastI
extraCycles = floor((1E12 - i) / cycleIters)
colScroll = colScroll + extraCycles * cycleHeight
colHeight = colHeight + extraCycles * cycleHeight
i = i + extraCycles * cycleIters
print "Fast-forwarded to i=" + i + ", colHeight=" + colHeight
memo = null
else
memo[key] = [i, colHeight]
end if
end if
add1Rock rocks[nextRockNum]
nextRockNum = (nextRockNum + 1) % rocks.len
i = i + 1
end while
print colHeight
The key for this memo map is the top 32 rows of the pit, all concatenated together, plus the current rock and gas numbers. We compute this key right before we drop each rock, and if we find that key already in our memo, it means we have found the start of a repeating cycle. It's going to just keep repeating over and over from there! So we can calculate how many times it will do that before the number of rocks approaches a trillion, and "fast forward" to that point by simply updating colScroll, colHeight, and i (our iteration number).
Here's the complete program for Part Two.
if 1 then fname = "input.txt" else fname = "example.txt"
gas = file.readLines(fname)[0]
nextGasNum = 0
column = [[]] * 7 // contents of each column of the pit
colHeight = 0 // total height (no longer equal to column[n].len)
colScroll = 0 // additional rows we've scrolled away
// Rock class: represents a Tetris-like block dropped in
Rock = {}
Rock.pattern = []
Rock.make = function(pattern)
noob = new Rock
noob.pattern = pattern
noob.width = pattern[0].len
noob.height = pattern.len
return noob
end function
Rock.hitsSomethingAt = function(x,y)
if x + self.width > 7 then return true
if x < 0 then return true
if y < 0 then return true
for row in self.pattern.indexes
if y + row >= colHeight then return false
p = self.pattern[self.height - 1 - row]
for col in p.indexes
if p[col] != "#" then continue
if column[x + col][y - colScroll + row] == "#" then return true
end for
end for
return false
end function
Rock.settle = function(x, y)
// first, grow all columns as needed
newHeight = y + self.height
if colHeight < newHeight then
for col in column.indexes
column[col] = column[col] + ["."] * (newHeight-colHeight)
end for
globals.colHeight = newHeight
if column[0].len > 200 then
globals.colScroll = colScroll + 100
for col in column.indexes
column[col] = column[col][100:]
end for
end if
end if
for row in self.pattern.indexes
p = self.pattern[self.height - 1 - row]
for col in p.indexes
if p[col] != "#" then continue
column[x + col][y - colScroll + row] = "#"
end for
end for
end function
rock0 = Rock.make(["####"])
rock1 = Rock.make([".#.", "###", ".#."])
rock2 = Rock.make(["..#", "..#", "###"])
rock3 = Rock.make(["#"]*4)
rock4 = Rock.make(["##", "##"])
rocks = [rock0, rock1, rock2, rock3, rock4]
add1Rock = function(rock)
// left edge 2 units away from left wall
x = 2
// bottom edge 3 units above highest rock (or floor)
y = colHeight + 3
while true
// apply gas
dir = gas[nextGasNum]
globals.nextGasNum = (nextGasNum + 1) % gas.len
if dir == ">" then
if not rock.hitsSomethingAt(x + 1, y) then
x = x + 1
end if
else
if not rock.hitsSomethingAt(x - 1, y) then
x = x - 1
end if
end if
// fall down
if rock.hitsSomethingAt(x, y - 1) then
// Settled!
rock.settle x, y
return
end if
y = y - 1
end while
end function
memo = {} // key: state key; value: [i, colHeight]
t0 = time
nextRockNum = 0
i = 0
while i < 1E12
if colHeight > 32 and memo != null then
keyParts = [nextRockNum, nextGasNum]
for col in column.indexes
keyParts.push column[col][-32:]
end for
key = keyParts.join("")
if memo.hasIndex(key) then
print "HEY!!! Found a cycle at i=" + i + " (colHeight=" + colHeight + ")"
print memo[key]
// Now we have a cycle, we can fast-forward to near a trillion.
lastI = memo[key][0]
lastHeight = memo[key][1]
cycleHeight = colHeight - lastHeight
cycleIters = i - lastI
extraCycles = floor((1E12 - i) / cycleIters)
colScroll = colScroll + extraCycles * cycleHeight
colHeight = colHeight + extraCycles * cycleHeight
i = i + extraCycles * cycleIters
print "Fast-forwarded to i=" + i + ", colHeight=" + colHeight
memo = null
else
memo[key] = [i, colHeight]
end if
end if
add1Rock rocks[nextRockNum]
nextRockNum = (nextRockNum + 1) % rocks.len
i = i + 1
end while
t1 = time
print colHeight
print "Time: " + (t1 - t0)
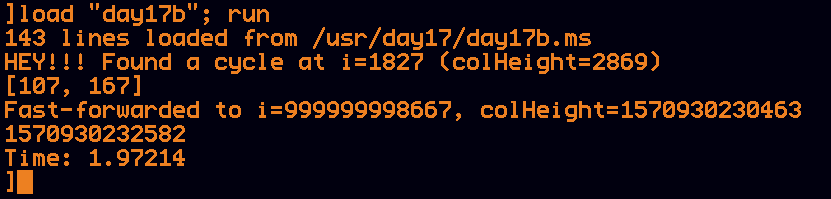
This runs in under 2 seconds, and calculated that a trillion blocks would stack up 1,570,930,232,582 rows high!
Conclusion
Part 1 took me 26 minutes to code up, and placed me 137th in the competition. Part 2, because I wasted so much time doubting the cycles idea, took another 39 minutes, and my rank at the end of that was 437.
MiniScript, however, performed like a champ. It handled the large numbers involved without breaking a sweat (or any special effort on my part). And this morning, I was able to make a minor enhancement to my program to generate the cool visualization you see here.
Want to play a real Tetris game in Mini Micro? Download this github repo, and follow the instructions in the Read Me. Then when you've played a bit, use the dir, load, and edit commands to poke at the code. Have fun!