Hey everyone! Welcome back to another day of problem-solving. It's day 37, and I'm still going strong on my quest for consistency. Today, we have an interesting problem to tackle. But before we dive in, let's make sure we're all on the same page.

Incase you are unfamiliar with graphs I suggest reading the previous article 32 && 33. It also contains the links to valuable resources.

Question: Topological sort

Given a Directed Acyclic Graph (DAG) with V vertices and E edges, Find any Topological Sorting of that Graph.

Example 1:

• 

• Output: 1

• Explanation: The output 1 denotes that the order is
  valid. So, if you have, implemented
  your function correctly, then output
  would be 1 for all test cases.
  One possible Topological order for the
  graph is 3, 2, 1, 0.

Example 2:

• 
• Output: 1
• Explanation: The output 1 denotes that the order is valid. So, if you have, implemented your function correctly, then output would be 1 for all test cases.
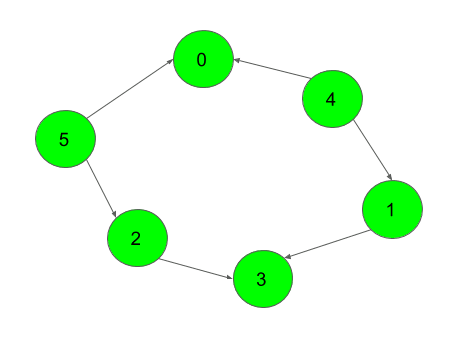
• One possible Topological order for the
• graph is 5, 4, 2, 1, 3, 0.

Constraints:

• 2 ≤ V ≤ 104
• 1 ≤ E ≤ (N*(N-1))/2

Intuition:

Let's start by understanding what topological sort means, what we require to output.
The topological sorting of a directed acyclic graph is nothing but the linear ordering of vertices such that if there is an edge between node u and v(u -> v), node u appears before v in that ordering.
Topological sort exists only in a directed acyclic graph.
Why directed? : In the case graph is undirected, two nodes representing 1 and 2, can be represented as {1,2} or {2,1}. We can't put any order to this as from either nodes we can traverse back to each other.

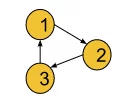
Why Acylic : If we try to get topological sorting of this cyclic graph, for edge 1->2, node 1 must appear before 2, for edge 2->3, node 2 must appear before 3, and for edge 3->1, node 3 must appear before 1 in the linear ordering. But such ordering is not possible as there exists a cyclic dependency in the graph. Thereby, topological sorting is only possible for a directed acyclic graph.

Algorithm:

• We will be solving it using DFS approach.
• What we are essentially going to do is we are going to maintain a visited array and a stack.
• We will call the dfs approach for all components of the graph.
• We will mark the visited node as 1 and then we will visit its adjacent nodes from the adjacency list.
• Incase we can't call the dfs for that path any more, then we will backtrack and push the values onto the stack.

Code:

class Solution
{
    public:
    void dfs(int node, vector<int> adj[], vector<int> &vis,  stack<int>& st){
        vis[node] = 1;

        for(auto it: adj[node]){
            if(!vis[it]){
                dfs(it,adj,vis,st);
            }
        }
        st.push(node);
    }
    //Function to return list containing vertices in Topological order. 
    vector<int> topoSort(int V, vector<int> adj[]) 
    {
        vector<int> vis(V,0);
        stack<int> st;

        for(int i = 0 ; i < V; i++){
            if(!vis[i]){
                dfs(i,adj,vis,st);
            }
        }
        vector<int> res;
        while(!st.empty()){
            res.push_back(st.top());
            st.pop();
        }
        return res;
    }
};

Complexity Analysis:

• Time Complexity: O(V+E) + O(V)
• Space Complexity: O(2N) + O(N)