Hey everyone! Welcome back to another day of problem-solving. It's day 44, and I'm still going strong on my quest for consistency. Today, We will be solving a problem using Floyd Warshall Algorithm.
So incase you don't know what that is, I suggest reading out this article: Floyd Warshall Algorithm.
Question: Find the City With the Smallest Number of Neighbors at a Threshold Distance
There are n cities numbered from 0 to n-1. Given the array edges where edges[i] = [fromi, toi, weighti] represents a bidirectional and weighted edge between cities fromi and toi, and given the integer distanceThreshold.
Return the city with the smallest number of cities that are reachable through some path and whose distance is at most distanceThreshold, If there are multiple such cities, return the city with the greatest number.
Notice that the distance of a path connecting cities i and j is equal to the sum of the edges' weights along that path.
Example 1:
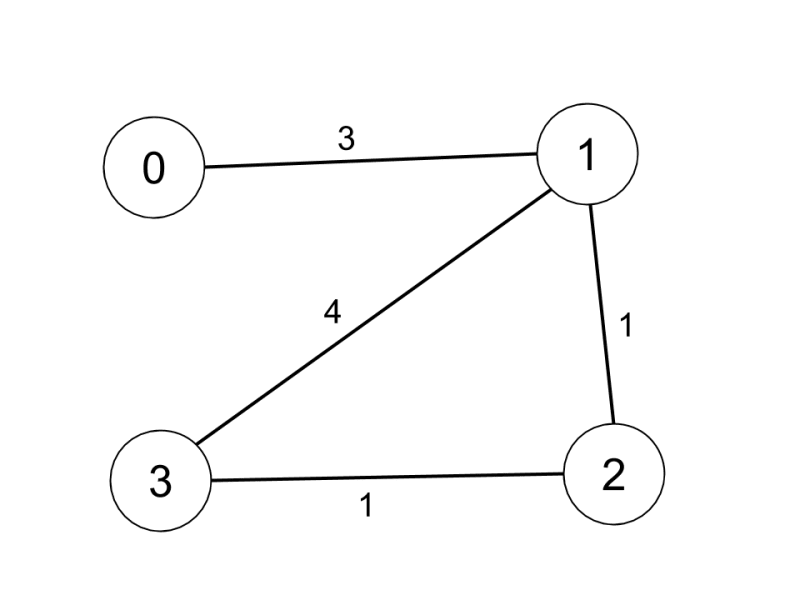
- Input: n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
- Output: 3
- Explanation: The figure above describes the graph. The neighboring cities at a distanceThreshold = 4 for each city are: City 0 -> [City 1, City 2] City 1 -> [City 0, City 2, City 3] City 2 -> [City 0, City 1, City 3] City 3 -> [City 1, City 2] Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.
Example 2:
- Input: n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
- Output: 0
- Explanation: The figure above describes the graph.
- The neighboring cities at a distanceThreshold = 2 for each city are:
- City 0 -> [City 1]
- City 1 -> [City 0, City 4]
- City 2 -> [City 3, City 4]
- City 3 -> [City 2, City 4]
- City 4 -> [City 1, City 2, City 3]
- The city 0 has 1 neighboring city at a distanceThreshold = 2.
Constraints:
2 <= n <= 100
1 <= edges.length <= n * (n - 1) / 2
edges[i].length == 3
0 <= fromi < toi < n
1 <= weighti, distanceThreshold <= 10^4
All pairs (fromi, toi) are distinct.
Intuition:
- So basically what we have been doing up until now is that we were finding the shortest path from one source node to a another source node using Dijkstra's Algorithm.
- It had few setbacks such as it could not be used when the weight was negative for an edge or it could not be used to detect a negative edge cycle as it would then go into a never ending loop.
- Here, Floyd Warshall algorithm helps us to generate a 2D matrix, that stores the shortest distances from each node to every other node. In the generated 2D matrix, each cell matrix[i][j] represents the shortest distance from node i to node j.
After generating the shortest distance from each node to each other we just run a loop through our result to count the no of cities with least adjacent cities than the threshold.
We can also use the Dijkstra's algorithm for this but we will have to use it for n nodes as we will have to calculate the shortest distance for each one.
Algorithm:
- Create a matrix of size n x n to represent the weighted directed graph. Initialize all entries to a maximum value (INT_MAX) to indicate no direct connection between cities.
- Iterate over the edges and update the matrix with the corresponding edge weights in both directions.
- Set the diagonal elements of the matrix to 0 to represent that each city has a distance of 0 from itself.
- Apply the Floyd-Warshall algorithm to find the shortest distances between all pairs of cities:
- Use three nested loops: the first loop (via) represents the intermediate city, and the second and third loops (i and j) represent the start and end cities.
- If the distances between i and via, and via and j are both finite (not INT_MAX), update the distance between i and j by taking the minimum of the current distance and the sum of distances via i and via j.
- Initialize variables cityCount as the total number of cities and ans as -1 (indicating no city found yet).
- Iterate over each city:
- Initialize cnt as 0 to count the number of cities within the distance threshold.
- Iterate over the nextCity and check if the distance between the current city and nextCity is less than or equal to the distanceThreshold. If so, increment cnt.
- If cnt is less than or equal to cityCount, update cityCount with cnt and ans with the current city index.
- Return ans as the index of the city with the smallest number of cities within the distance threshold.
Variable Explanation:
- n: Represents the total number of cities.
- edges: Stores the connections between cities along with their weights.
- distanceThreshold: Represents the maximum allowed distance to consider a city within the threshold.
- matrix: Represents the adjacency matrix of the directed graph, where matrix[i][j] stores the weight of the edge between city i and city j.
- cityCount: Stores the minimum count of cities within the distance threshold encountered so far.
- ans: Stores the index of the city with the smallest number of cities within the distance threshold.
Code:
int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
//making of directed graph
vector<vector<int>> matrix(n,vector<int>(n,INT_MAX));
for(auto it: edges){
matrix[it[0]][it[1]] = it[2];
matrix[it[1]][it[0]] = it[2];
}
for(int i = 0; i < n; i++){
matrix[i][i] = 0;
}
for(int via = 0; via < n; via++){
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
if(matrix[i][via] == INT_MAX || matrix[via][j] == INT_MAX) continue;
matrix[i][j] = min(matrix[i][j], matrix[i][via] + matrix[via][j]);
}
}
}
int cityCount = n;
int ans = -1;
for(int i = 0; i < n; i++){
int cnt = 0;
for(int nextCity = 0; nextCity < n; nextCity++){
if(matrix[i][nextCity] <= distanceThreshold) cnt++;
}
if(cnt <= cityCount){
cityCount = cnt;
ans = i;
}
}
return ans;
}
Complexity Analysis:
Time: O(N^3)
Space: O(N^2)