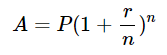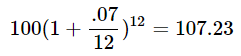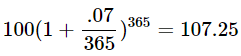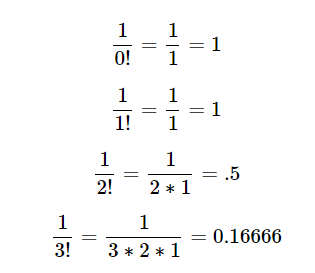I just learned something new and it prompted me to want to share it (and a whole bunch of other things). Let's talk about the letter e. This post will have a little bit of math in it (possibly a lot), but I'll try to make those parts painless enough to keep you with me.

e

e is a mathmatical constant (like pi) that crops up a lot of places.

Like pi, it's a number that is irrational, meaning that its decimal places never end and never repeat (go into an infinite loop).

"Blah blah blah blah," you say -- eloquently, I might add. "All I hear is blah blah math letters-that-are-really-numbers blah. Why are you bothering me about this e?"

I want to tell you about it, because, even though it doesn't get the kind of press that pi does (not to mention phi -- the golden ratio), it shows up everywhere you look and helps us with all kinds of statistics, finance, and more! I'm writing this post to show off a couple of the ways that e works behind the scenes.

Something Interesting and Practical

Let's talk about interest. Like bank interest! Like investment stocks interest. You ever wonder how that was calculated? Here's the interest equation:

Where:

A is the future value of your money.

P is the present value of your money.

r is the interest rate over the time period you care about (usually a year, in practice).

n is the number of times you compound your interest over the time period.

For example, if you put $100 into a bank for a year, and the bank provided a 7% (or .07) interest rate over that time, and the bank only compounded your interest one time (which they sometimes do), after one year, you'd end up with:

This is as expected, because we already said you're getting 7% yearly interest (also known as APR), and 7% of 100 is 7, so getting $107 at the end of the year should hopefully seem reasonable.

But some banks compound your interest every month! Check your bank statement -- yours probably does! What does that look like?

WHAAAAAAT? You just got an extra $0.23, simply by doing some math 12 times a year instead of once at the end. You squint at me skeptically, and ask, "Does that pattern continue like that?" Let's try it! Let's compound once a day.

Yep! Kind of. Definitely not as much increase, and we're compounding waaaay more. Let's really amp up the compounding and see what happens.

Actually, let's simplify our life a little bit first to make the math easy:

1. Let's assume we're starting with just $1.
2. Let's assume our interest rate is 100% (i.e. 1). Thus compounding yearly, we would double our money.

Now let's see what our pattern looks like.

r = 1.0
p = 1.0

def compound(p, r, n):
    """Calculates interest after one time period (e.g. a year).
    p: float - initial money amount
    r: float - interest rate over the time period
    n: int - number of times we compound
    returns float - amount of money after one time period
    """
    return p*((1 + r/n)**n)

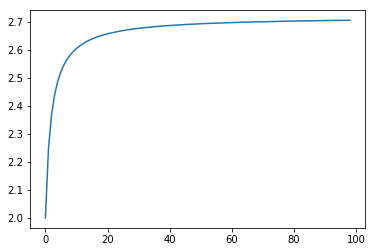
result_data = [compound(p, r, n) for n in range(1, 100)]

from matplotlib import pyplot as plt
plt.plot(result_data)
plt.show()

You can see that with 1 compound, we get 100% return, just like we planned. Start with $1, end up with $2. And as we compound more and more, we see it go up by quite a bit and then the gains start to level off. But wait. What number are the gains leveling off at?

from math import e
plt.plot((0, 100), (e, e))  # Plot horizontal line at 2.71828...
plt.plot(result_data)
plt.show()

OH SNAP, IT'S E. As we approach higher and higher frequency of compounding, we approach a return amount of E. This is where the concept of continuously compounding interest comes from. If you want more details and less hand-waving, have a look at these slides. They do a great job of explaining things slowly, simply, and with lots of examples.

So we've found e once. Let's do another.

Factorials and e

If you've read any of my other blog posts, you're probably sick and tired of factorials. Well, that's too bad. Let's combine them with fractions and see what we can come up with.

Where am I going with this? Let's add them up and see.

from math import factorial

def sum_of_factorial_fractions(n):
    """Calculates the sum of 1/0! + 1/1! + 1/2! ... 1/n!"""
    return sum(1/factorial(x) for x in range(0, n + 1))

results2 = [sum_of_factorial_fractions(n) for n in range(10)]
plt.plot(results2)
plt.show()
print("The last result:", results2[-1])

The last result: 2.7182815255731922

A;LSDKJF;ALKJSDFJSDLKFJEIVLENNVOIEJ.

E

(approximately).

Let's do one more: my favorite one.

Random E

This one comes courtesy of Fermat's Library on Twitter. Pick a random number between 0 and 1. Keep picking numbers and adding them until the sum is greater than 1. For example:

from random import random
x = random()
print(x)

0.185263666584764

x += random()
print(x)

0.5797470876977189

x += random()
print(x)

1.2821236982804123

Alright! We're now greater than 1, and it took us 3 rolls to get there. Let's do that a ton of times and see what the average number of rolls is.

def rolls_to_greater_than_n(n):
    """Rolls a random number between 0 and 1 and adds them up
    until the sum is greater than n.  Returns the number of rolls it took.
    """
    total = 0
    rolls = 0
    while total < n:
        total += random()
        rolls += 1
    return rolls

def roll_experiment_avg(n, times):
    """Performs the rolls_to_greater_than_n 'times' times.
    Returs the average number of rolls it took."""
    return sum(rolls_to_greater_than_n(n) for _ in range(times))/times

results3 = [roll_experiment_avg(1, x) for x in range(1, 10000)]
plt.plot(results3)
plt.plot((0, 10000), (e, e))  # Line representing e for reference.
plt.show()
print("The last result was", results3[-1])

The last result was 2.712271227122712

This one definitely is converging a lot slower, but it does. Math says so.

Anyways, this was kind of a long post about nothing, but I though that the way that e seems to pop up all over the place, even amidst factorials and random numbers, was pretty cool. Let me know if you can think of any other cool ways to come up with e!

Originally posted on assert_not magic?