Disclosure: This post includes affiliate links; I may receive compensation if you purchase products or services from the different links provided in this article.
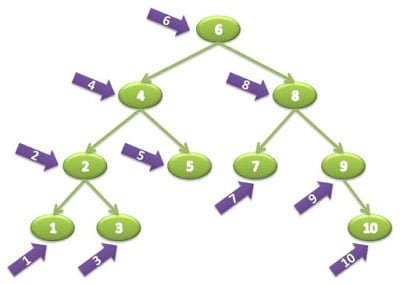
The InOrder traversal is one of the three popular ways to traverse a binary tree data structure, the other two being the preOrder and postOrder. During the in-order traversal algorithm, the left subtree is explored first, followed by root, and finally nodes on the right subtree.
You start traversal from root then goes to the left node, then again goes to the left node until you reach a leaf node. At that point in time, you print the value of the node or mark it visited and moves to right subtree. Continuing the same algorithm until all nodes of the binary tree are visited. The InOrder traversal is also known as left-node-right or left-root-right traversal or LNR traversal algorithm.
Similar to the preOrder algorithm, it is also a depth-first algorithm because it explores the depth of a binary tree before exploring siblings. Since it is one of the fundamental binary tree algorithms it's quite popular in programming interviews.
These traversal algorithms are also the basis to learn more advanced binary tree algorithms, hence every programmer should learn, understand and know how to implement in-order and other traversal algorithms.
The easiest way to implement the inOrder traversal algorithm in Java or any programming language is by using recursion. Since the binary tree is a recursive data structure, recursion is the natural choice for solving a tree-based problem. The inOrder() method in the BinaryTree class implements the logic to traverse a binary tree using recursion.
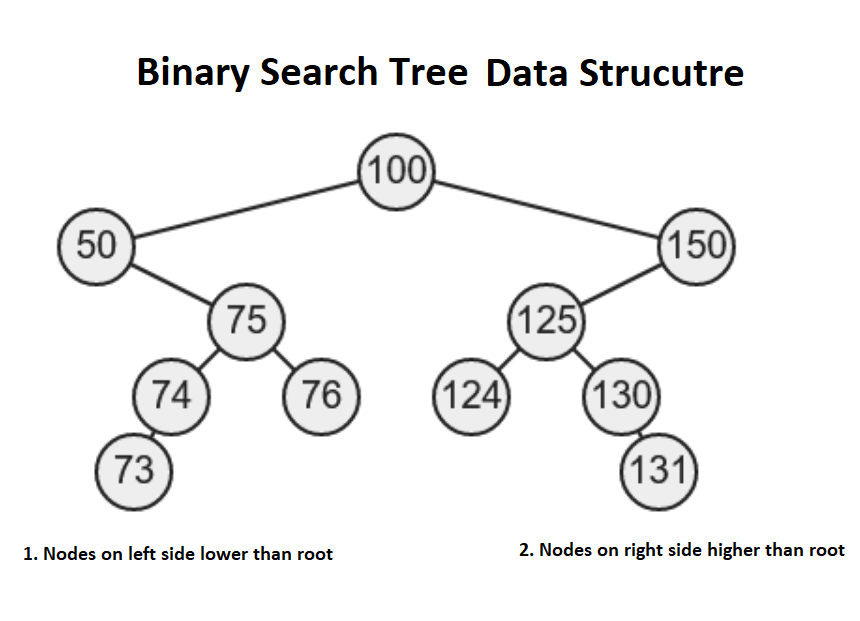
From Interview point of view, InOrder traversal is extremely important because it also prints nodes of a binary search tree in the sorted order but only if given tree is binary search tree. If you remember, in BST, the value of nodes in left subtree is lower than the root and values of nodes on right subtree is higher than root. The In order traversal literally means IN order i.e notes are printed in the order or sorted order.
Btw, even though these three algorithms (pre-order, in-order, and post-order) are popular binary tree traversal algorithms but they are not the only ones. You also have other breadth-first ways to traverse a binary tree e.g. level order traversal (See Data Structure and Algorithms: Deep Dive).
The recursive algorithm to implement InOrder traversal of a Binary tree
The recursive algorithm of inorder traversal is very simple. You just need to call the inOrder() method of BinaryTree class in the order you want to visit the tree. What is most important is to include base case, which is key to any recursive algorithm.
For example, in this problem, the base case is you reach to the leaf node and there is no more node to explore, at that point of time recursion starts to wind down. Here are the exact steps to traverse binary tree using InOrder traversal:
- visit left node
- print value of the root
- visit right node\ and here is the sample code to implement this algorithm using recursion in Java:
private void inOrder(TreeNode node) {
if (node == null) {
return;
}
inOrder(node.left);
System.out.printf("%s ", node.data);
inOrder(node.right);
}
Similar to preOrder() method in the last example, there is another inOrder() method which exposes inorder traversal to the public and calls this private method which actually performs the InOrder traversal.
This is the standard way to write a recursive method which takes input, it makes it easier for a client to call the method.
public void inOrder() {
inOrder(root);
}
You can see that we start with root and then recursive call the inOrder() method with node.left, which means we are going down on left subtree until we hit node == null, which means the last node was a leaf node.
At this point in time, the inOrder() method will return and execute the next line, which prints the node.data. After that its again recursive inOrder() call with node.right, which will initiate the same process again.
You can also check out Data Structure and Algorithms Part 1 and 2 courses on Pluralsight to learn more about algorithms and how to design your own algorithms.
Btw, you would need a Pluralsight membership to access this course, which costs around $29 monthly or $299 annually (14% saving). I have one and I also suggest all developers have that plan because Pluralsight is like NetFlix for Software developers.
It has more than 5000+ good quality courses on all latest topics. Since we programmers have to learn new things every day, an investment of $299 USD is not bad.
Btw, it also offers a 10-day free trial without any obligation which allows you to watch 200 hours of content. You can watch these courses for free by signing for that 10-day free trial.
InOrder traversal of a Binary tree in Java
Here is our complete solution of inorder traversal algorithm in Java. This program uses a recursive algorithm to print the value of all nodes of a binary tree using InOrder traversal.
As I have told you before, during in-order traversal value of left subtree is printed first, followed by root and right subtree. If you are interested in the iterative algorithm, you can further check this tutorial of implementing in order traversal without recursion.
import java.util.Stack;
/*
* Java Program to traverse a binary tree
* using inorder traversal without recursion.
* In InOrder traversal first left node is visited, followed by root
* and right node.
*
* input:
* 40
* /\
* 20 50
* / \\
* 10 30 60
* / /\
* 5 67 78
*
* output: 5 10 20 30 40 50 60 67 78
*/
public class Main {
public static void main(String[] args) throws Exception {
// construct the binary tree given in question
BinaryTree bt = BinaryTree.create();
// traversing binary tree using InOrder traversal using recursion
System.out
.println("printing nodes of binary tree on InOrder using recursion");
bt.inOrder();
}
}
class BinaryTree {
static class TreeNode {
String data;
TreeNode left, right;
TreeNode(String value) {
this.data = value;
left = right = null;
}
}
// root of binary tree
TreeNode root;
/**
* traverse the binary tree on InOrder traversal algorithm
*/
public void inOrder() {
inOrder(root);
}
private void inOrder(TreeNode node) {
if (node == null) {
return;
}
inOrder(node.left);
System.out.printf("%s ", node.data);
inOrder(node.right);
}
/**
* Java method to create binary tree with test data
*
* @return a sample binary tree for testing
*/
public static BinaryTree create() {
BinaryTree tree = new BinaryTree();
TreeNode root = new TreeNode("40");
tree.root = root;
tree.root.left = new TreeNode("20");
tree.root.left.left = new TreeNode("10");
tree.root.left.left.left = new TreeNode("5");
tree.root.left.right = new TreeNode("30");
tree.root.right = new TreeNode("50");
tree.root.right.right = new TreeNode("60");
tree.root.left.right.left = new TreeNode("67");
tree.root.left.right.right = new TreeNode("78");
return tree;
}
}
Output
printing nodes of binary tree on InOrder using recursion
5 10 20 30 67 78 40 50 60
That's all about how to implement inOrder traversal of a binary tree in Java using recursion. You can see the code is pretty much similar to the preOrder traversal with the only difference in the order we recursive call the method. In this case, we call inOrder(node.left) first and then print the value of the node.
It's worth remembering that in order traversal is a depth-first algorithm and prints tree node in sorted order if given binary tree is a binary search tree.
In the next part of this article, I'll share inOrder traversal without recursion, meanwhile, you can try practicing following data structure and binary tree problems.
Further Learning
Data Structures and Algorithms: Deep Dive Using Java
Algorithms and Data Structures - Part 1 and 2
Data Structures in Java 9 by Heinz Kabutz
Cracking the Coding Interview - 189 Questions and Solutions
Grokking the Coding Interview: Patterns for Coding Questions
100+ Data Structure and Algorithms Questions for Programmers
75+ Programming and Coding Interview Questions
Other data structure and algorithms tutorials for Java Programmers
- 10 Algorithm books Every Programmer Should Read (list)
- How to implement Quicksort algorithm in Java? (solution)
- 5 Books to learn data structure and algorithms in Java? (books)
- How to implement a binary search algorithm in Java? (solution)
- How to find all pairs on integer array whose sum is equal to given a number? (solution)
- How to reverse an array in place in Java? (solution)
- How to reverse a linked list in Java without recursion? (solution)
- How to implement Insertion sort in Java? (solution)
- How to find the missing number in an array of 1 to 100? (solution)
- How to find the length of a singly linked list in Java? (solution)
- 15 frequently asked data structure and algorithm Interview Questions (list)
If you have any suggestion to make this algorithm better, feel free to suggest. Interviewer loves people who come up with their own algorithm or give some touch to popular algorithms.
P.S. - If you don't mind learning from free resources then you can also take a look at my list of free data structure and algorithm courses for Java developers.