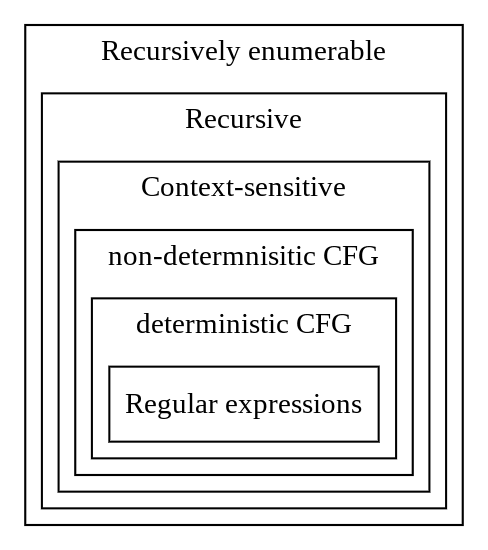
Chomsky hierarchy
| Grammar | Languages | Automaton | Complexity |
|---|---|---|---|
| Type-0 | Recursively enumerable | Turing machine | undecidable |
| Type-0 | Recursive | ||
| Type-1 | Context-sensitive | Linear-bounded non-deterministic Turing machine | exponential |
| Type-2 | non-determnisitic CFG | Non-deterministic pushdown automaton | polynomial |
| Type-2 | deterministic CFG | Deterministic pushdown automaton | |
| Type-3 | Regular expressions | Finite state automaton | linear |
Note : CFG - context-free grammars; REG - regular expressions; CSG - context-sensitive grammars; DFA - deterministic finite automaton;
Chomsky initially identified 4 types in his hierarchy, but then we discovered correspondence between language hierarchies and computational complexity. So we can refine initial categorization with more classes, for example mildly context-sensitive.
Side note: diagram of the world of computability and complexity, complexity zoology: active inclusion diagram, complexity zoo, computational complexity theory at SEP.
Regular expressions can’t specify, for example:
- Palindromes
- Strings with an equal number of 0’s and 1’s
- Matched parentheses
- Properly formed arithmetic expressions
REG is not enough for a general programming language ( PL ), CSG is too much (it is exponential), so the default choice for PL is CFG. BNF is used to formally specify PL (which is non-deterministic CFG), but I would say that deterministic CFG is preferred for parsing, for example, PEG.
Side note: What’s the Difference Between BNF, EBNF, ABNF?, On the Expressive Power of Programming Languages by Shriram Krishnamurthi.
Tasks
Non-deterministic CFG algorithms useful for natural language processing, but they tend to be slower (and non-deterministic, obviously). For PL parsing deterministic CFG seems to be more practical - they can be less expressive, but faster and much simpler to implement. This is the key idea of PEG parser, it is deterministic by construction and not left recursive (but it is always possible to rewrite from left-recursive form to right recursive).
Typical tasks for programs working with deterministic CFG are:
- Identify if a given sentence is a member of language or not, for example, validate the email
- Generate valid sentences for a given language, for example, generate fake emails
- Parse given sentence, for example, generate AST for compiler/interpreter or highlight syntax
Current research:
- Parallel parsing algorithms - mainly for non-deterministic CFG
- Streaming parsers - to parse input from a socket
- Error recovery, for better error messages or to be able to highlight syntax in presence of an error
- Incremental parsing, for example, to be able to do syntax highlighting in IDE on each keystroke. See tree-sitter
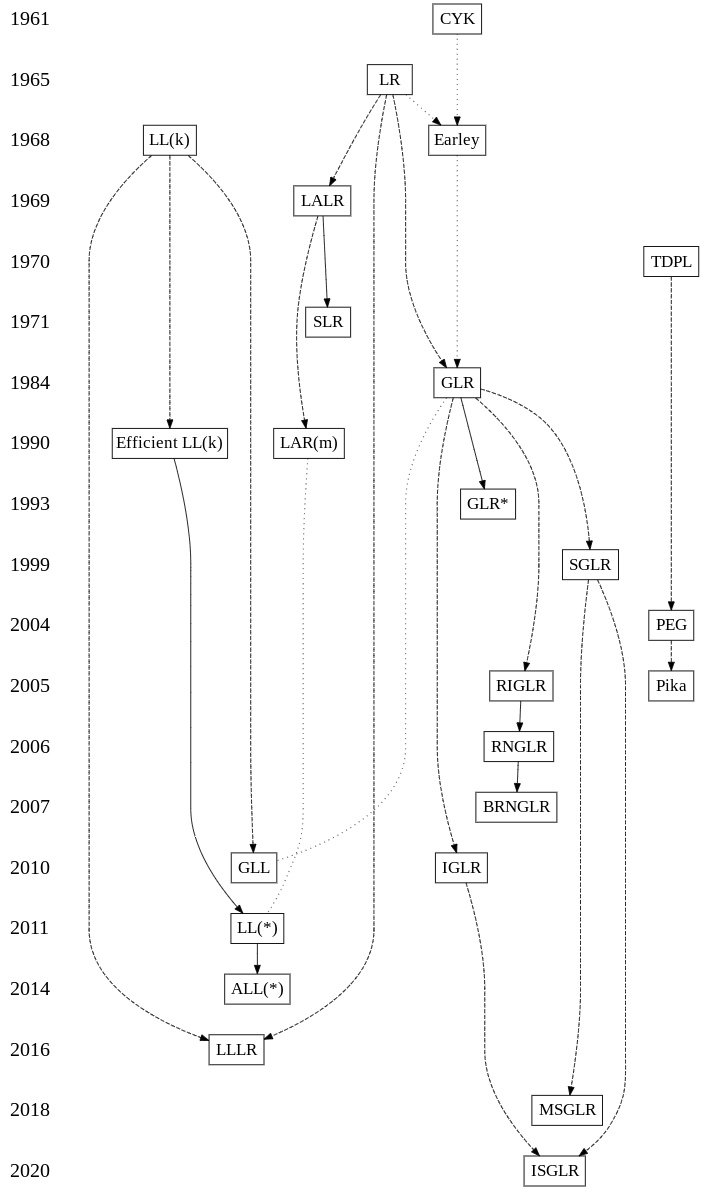
Algorithms
Parser users tend to separate themselves into bottom-up and top-down tribes. Top-down users value the readability of recursive descent (
RD) implementations ofLLparsing along with the ease of semantic action incorporation. Bottom-up users value the extended parsing power ofLRparsers, in particular the admissibility of left recursive grammars, althoughLRparsers cannot cope with hidden left recursion and evenLR(0)parse tables can be exponential in the size of the grammar, while anLLparser is linear in the size of the grammar.
List of algorithms (based on this page):
-
CYK(Cocke–Younger–Kasami) algorithm- bottom-up, dynamic programming, chart parser
- supports any context-free grammar in Chomsky Normal Form
O(n^3)- online demo 1, online demo 2, list of part-of-speech tags
-
Earleyparser (Jay Earley, 1968):- dynamic programming, chart parser
- supports any context-free grammar
O(n^3)
Earleygave an outline of a method for turning his recognizers into parsers, but it turns out that this method is incorrect. Tomita’sGLRparser returns a shared packed parse forest (SPPF) representation of all derivations of a given string from a given CFG but is worst-case unbounded polynomial order. – SPPF-Style Parsing From Earley Recognisers
LL
left-to-right, leftmost derivation (top-down), “recursive descent”
-
LL(k)(Lewis and Stearns, 1968)-
ktokens of lookahead - very expensive (when introduced)
-
-
LL(1)- exactly one token lookahead
- much more efficient
- uses
FIRST()andFOLLOW()to build parse tables - online demo 1, online demo 2
-
Efficient LL(k)(Terence Parr, 1990)-
ktokens of lookahead -
kis gradually increased w/ backtracking as a failback - basis of original
ANTLR
-
In terms of recognition strength,
LLtechniques are widely held to be inferior toLRparsers. The fact that anyLR(k)grammar can be rewritten to beLR(1), whereasLL(k)is stronger thanLL(1), appears to giveLRtechniques the additional benefit of not requiring k-token lookahead and its associated ovehead. In this paper, we suggest thatLL(k)is actually superior toLR(1)when translation, rather than acceptance, is the goal. Further, a practical method of generating efficientLL(k)parsers is presented. This practical approach is based on the fact that most parsing decisions in a typicalLL(k)grammar can be made without comparing k-tuples and often do not even require the full k tokens of look ahead. We denote such"optimized" LL(k)parsers
-
GLLGeneralisedLL(Bernard Lang, 1974 & Scott and Johnstone, 2010)-
LLanalogue toGLR - maintains multiple parsing descriptors on a stack
-
Recursive Descent (RD) parsers are popular because their control flow follows the structure of the grammarand hence they are easy to write and to debug. However, the class of grammars which admit RD parsersis very limited. Backtracking techniques may be used to extend this class, but can have explosive run-times and cannot deal with grammars with left recursion. Tomita-style
RNGLRparsers are fully generalbut are based onLRtechniques and do not have the direct relationship with the grammar that an RD parser has. We develop the fully generalGLLparsing technique which is recursive descent-like, and has the property that the parse follows closely the structure of the grammar rules, but usesRNGLR-like machinery to handle non-determinism. The resulting recognisers run in worst-case cubic time and can be built evenfor left recursive grammars.
-
LL(*)(Terence Parr and Kathleen Fisher, 2011)-
LLanalogue toLAR(m) - regular lookaheads w/ cyclic DFAs
- basis of original
ANTLR 3(?)
-
Despite the power of Parser Expression Grammars (
PEGs) andGLR, parsing is not a solved problem. Adding nondeterminism (parser speculation) to traditionalLLandLRparsers can lead to unexpected parse-time behavior and introduces practical issues with error handling, single-step debugging, and side-effecting embedded grammar actions. This paper introduces theLL(*)parsing strategy and an associated grammar analysis algorithm that constructsLL(*)parsing decisions from ANTLR grammars. At parse-time,decisions gracefully throttle up from conventional fixed k≥1 lookahead to arbitrary lookahead and, finally, fail over to backtracking depending on the complexity of the parsing decision and the input symbols.LL(*)parsing strength reaches into the context-sensitive languages, in some cases beyond whatGLRandPEGs can express. By statically removing as much speculation as possible,LL(*)provides the expressivity ofPEGs while retainingLL’s good error handling and unrestricted grammar actions.
-
ALL(*)AdaptiveLL(*)(Parsing: The Power of Dynamic Analysis” Terence Parr, Sam Harwell, and Kathleen Fisher 2014)- parallel regular lookaheads
- dynamic; adapts to input sentences
- simulates augmented recursive transition networks (ATNs)
- basis of
ANTLR 4
Despite the advances made by modern parsing strategies suchas
PEG,LL(*),GLR, andGLL, parsing is not a solved problem. Existing approaches suffer from a number of weaknesses, including difficulties supporting side-effecting embedded actions, slow and/or unpredictable performance, and counter-intuitive matching strategies. This paper introduces theALL(*)parsing strategy that combines the simplicity, efficiency, andpredictability of conventional top-downLL(k)parsers with the power of aGLR-like mechanism to make parsing decisions. The critical innovation is to move grammar analysis to parse-time, which letsALL(*)handle any non-left-recursive context-free grammar.ALL(*)is O(n4) in theory but consistently performs linearly on grammars used in practice, outperform in ggeneral strategies such asGLLandGLRby orders of magnitude. ANTLR 4 generatesALL(*)parsers and supports directleft-recursion through grammar rewriting.
A new parsing method called
LLLRparsing is defined and a method for producingLLLRparsersis described. AnLLLRparser uses anLLparser as its backbone and parses as much of itsinput string usingLLparsing as possible. To resolveLLconflicts it triggers small embeddedLRparsers. An embeddedLRparser starts parsing the remaining input and once theLLconflict is resolved, theLRparser produces the left parse of the substring it has just parsed and passes the control back to the backboneLLparser. TheLLLR(k)parser can be constructed for anyLR(k)grammar. It produces the left parse of the input string without any backtracking and, if used for a syntax-directed translation, it evaluates semantic actions using the top-down strategy just like the canonicalLL(k)parser. AnLLLR(k)parser is appropriate for grammars where theLL(k)conflicting nonterminals either appear relatively close to the bottom of the derivation trees or produce short substrings. In such cases anLLLRparser can perform a significantly better error recovery than anLRparser since the most part of the input string is parsed with the backboneLLparser.LLLRparsing is similar toLL(∗)parsing except that it (a) usesLR(k)parsers insteadof finite automata to resolve theLL(k)conflicts and (b) does not perform any backtracking.
LR
left-to-right, rightmost derivation (“bottom-up”), “shift/reduce”
- Canonical
LR(Don Knuth, 1965)- allows duplicated states
- fewer conflicts; much larger parse tables
- online demo
-
SLR(Frank DeRemer)- simple
LR:LR(0)states and their transitions -
FOLLOW()used to compute lookaheads - online demo
- simple
-
LALR(Frank DeRemer, 1969)- similar to
SLRbut w/ smaller lookaheads - equivalently, a simplified version of canonical
LR - more complicated lookahead calculation
- basis of yacc/bison
- recursive ascent (Thomas Penello, 1986)
- online demo
- similar to
-
GLR(Masaru Tomita, 1984)- generalized
LR(k): returns all valid parses - spawns parallel parsing processes on conflicts
- graph-structured stack (
GSS) - more efficient than Earley
- generalized
-
LAR(m)(Practical arbitrary lookahead LR parsing, Bermudez and Schimpf, 1990)- regular lookaheads w/ cyclic DFAs
-
GLR*(GLR* - An Efficient Noise-skipping Parsing Algorithm For Context Free Grammars Alon Lavie and Masaru Tomita, 1993) -
SGLRScannerlessGLR(Scannerless generalized-LR parsing, Eelco Visser, 1999)
Current deterministic parsing techniques have a number of problems. These include the limitations of parser generators for deterministic languages and the complex interface between scanner and parser. Scannerless parsing is a parsing technique in which lexical and context-free syntax are integrated into one grammar and are all handled by a single context-free analysis phase. This approach has a number of advantages including discarding of the scanner and lexical disambiguation by means of the context in which a lexical token occurs. Scannerless parsing generates a number of interesting problems as well. Integrated grammars do not fit the requirements of the conventional deterministic parsing techniques. A plain context-free grammar formalism leads to unwieldy grammars, if all lexical information is included. Lexical disambiguation needs to be reformulated for use in context-free parsing. The
scannerless generalized-LRparsing approach presented in this paper solves these problems. Grammar normalization is used to support an expressive grammar formalism without complicating the underlying machinery. Follow restrictions are used to express longest match lexical disambiguation. Reject productions are used to express the prefer keywords rule for lexical disambiguation. TheSLR(1)parser generation algorithm is adapted to implement disambiguation by general priority and associativity declarations and to interpret follow restrictions.Generalized-LRparsing is used to provide dynamic lookahead and to support parsing of arbitrary context-free grammars including ambiguous ones. An adaptation of theGLRalgorithm supports the interpretation of grammars with reject productions.
-
RIGLRReduction Incorporated GeneralizedLR(Elizabeth Scott and Adrian Johnstone. Generalised bottom up parsers with reduced stack activity, 2005)
We describe a generalized bottom up parser in which non-embedded recursive rules are handled directly by the underlying automaton, thus limiting stack activity to the activation of rules displaying embedded recursion. Our strategy is motivated by Aycock and Horspool’s approach, but uses a different automaton construction and leads to parsers that are correct for all context-free grammars, including those with hidden left recursion. The automaton features edges which directly connnect states containing reduction actions with their associated goto state: hence we call the approach reduction incorporated generalized LR parsing. Our parser constructs shared packed parse forests in a style similar to that of Tomita parsers. We give formal proofs of the correctness of our algorithm, and compare it with Tomita’s algorithm in terms of the space and time requirements of the running parsers and the size of the parsers’ tables.
-
RNGLRRight nulledGLRparsers (Elizabeth Scott and Adrian Johnstone. Right nulled GLR parsers, 2006)
The right nulled generalized
LRparsing algorithm is a new generalization ofLRparsing which provides an elegant correction to, and extension of, Tomita’sGLRmethods whereby we extend the notion of a reduction in a shift-reduce parser to include right nulled items. The result is a parsing technique which runs in linear time onLR(1)grammars and whose performance degrades gracefully to a polynomial bound in the presence of nonLR(1)rules. Compared to otherGLR-based techniques, our algorithm is simpler and faster.
-
BRNGLRBinary Right Nulled GLR (BRNGLR: a cubic Tomita-style GLR parsing algorithm, Elizabeth Scott, Adrian Johnstone, Rob Economopoulos, 2007)
Tomita-style generalised
LR(GLR) algorithms extend the standardLRalgorithm to non-deterministic grammars by performing all possible choices of action. Cubic complexity is achieved if all rules are of length at most two. In this paper we shall show how to achieve cubic time bounds for all grammars by binarising the search performed whilst executing reduce actions in aGLR-style parser. We call the resulting algorithm Binary Right NulledGLR(BRNGLR) parsing. The binarisation process generates run-time behaviour that is related to that shown by a parser which pre-processes its grammar or parse table into a binary form, but without the increase in table size and with a reduced run-time space overhead. BRNGLR parsers have worst-case cubic run time on all grammars, linear behaviour onLR(1)grammars and produce, in worst-case cubic time, a cubic size binary SPPF representation of all the derivations of a given sentence.
A major research goal for compilers and environments is the automatic derivation of tools from formal specifications. However, the formal model of the language is often inadequate; in particular,
LR(k)grammars are unable to describe the natural syntax of many languages, such as C++ and Fortran, which are inherently non-deterministic. Designers of batch compilers work around such limitations by combining generated components with ad hoc techniques (for instance, performingpartial type andscope analysis in tandem with parsing). Unfortunately, thecomplexity of incremental systems precludes the use of batch solutions. The inability to generate incremental tools for important languages inhibits the widespread use of language-rich interactive environments. We address this problem by extending the language model itself, introducing a program representation based on parse DAGs that is suitable for both batch and incremental analysis. Ambiguities unresolved by one stage are retained in this representation until further stages can complete the analysis, even if the resolution depends on further actions by the user. Representing ambiguity explicitly increases the number and variety of languages that can be analyzed incrementally using existing methods.
-
MSGLRModularSGLR(A Modular SGLR Parsing Architecture for Systematic Performance Optimization, Denkers, Jasper et al., 2018)
SGLRparsing is an approach that enables parsing of context-free languages by means of declarative, concise and maintainable syntax definition. Existing implementations suffer from performance issues and their architectures are often highly coupled without clear separation between their components. This work introduces a modularSGLRarchitecture with several variants implemented for its components to systematically benchmark and improve performance. This work evaluates these variants both independently and combined using artificial and real world programming languages grammars. The architecture is implemented in Java as JSGLR2, the successor of the original parser in Spoofax, interpreting parse tables generated by SDF3. The improvements combined result into a parsing and imploding time speedup from 3x on Java to 10x on GreenMarl with respect to the previous JSGLR implementation.
We present the Incremental Scannerless Generalized
LR(ISGLR) parsing algorithm, which combines the benefits ofIncremental GeneralizedLR(IGLR) parsing and Scanner-less Generalized LR (SGLR) parsing. TheISGLRparser canreuse parse trees from unchanged regions in the input andthus only needs to parse changed regions. We also presentincremental techniques for imploding the parse tree to anAbstract Syntax Tree (AST) and syntax highlighting. Scan-nerless parsing relies heavily on non-determinism duringparsing, negatively impacting the incrementality ofISGLRparsing. We evaluated theISGLRparsing algorithm usingfile histories from Git, achieving a speedup of up to 25 timesover non-incrementalSGLR
PEG
-
TDPLorTS(The tmg recognition schema, Alexander Birman, 1970) -
PEG: parsing expression grammar (Parsing Expression Grammars: A recognition-based Syntactic Foundation, Bryan Ford, 2004)- similar to CFG-based grammars, but alternation is inherently ordered
- often implemented with “packrat” parsers that memoize partial results
For decades we have been using Chomsky’s generative system of grammars,particularly context-freegrammars(CFGs)and regular expressions(REs),to express the syntax of programming languages and protocols. The power of generative grammars to express ambiguity is crucial to their original purpose of modelling natural languages, but this very power makes it unnecessarily difficult both to express and to parse machine-oriented languages using CFGs. Parsing Expression Grammars(
PEGs) provide an alternative recognition-based formal foundation for describing machine-oriented syntax,which solves the ambiguity problem by not introducing ambiguity in the first place Where CFG sexpress nondeterministic choice between alternatives,PEGs instead use prioritized choice.PEGs address frequently felt expressiveness limitations of CFGs and REs, simplifying syntax definitions and making it unnecessary to separate their lexical and hierarchical components. A linear-time parser can be built for any PEG , avoiding both the complexity and fickleness ofLRparsers and the inefficiency of generalized CFG parsing.While PEGs provide a rich set of operators for constructing grammars, they are reducible to two minimal recognition schemas developed around 1970,TS/TDPLandgTS/GTDPL, which are here proven equivalent ineffective recognition power.
A recursive descent parser is built from a set of mutually-recursive functions, where each function directly implements one of thenonterminals of a grammar. A
packratparser uses memoization to reduce the time complexity for recursive descent parsing fromexponential to linear in the length of the input. Recursive descent parsers are extremely simple to write, but suffer from two significantproblems: (i) left-recursive grammars cause the parser to get stuck in infinite recursion, and (ii) it can be difficult or impossible to optimally recover the parse state and continue parsing after a syntax error. Both problems are solved by thepikaparser, a novel reformulation ofpackratparsing as a dynamic programming algorithm, which requires parsing the input in reverse: bottom-up andright to left, rather than top-down and left to right. This reversed parsing order enablespikaparsers to handle grammars that use eitherdirect or indirect left recursion to achieve left associativity, simplifying grammar writing, and also enables optimal recovery fromsyntax errors, which is a crucial property for IDEs and compilers.Pikaparsing maintains the linear-time performance characteristics ofpackratparsing as a function of input length. Thepikaparserwas benchmarked against the widely-used Parboiled2 and ANTLR4 parsing libraries, and the pikaparserperformed significantly better than the otherparsersfor an expression grammar, althoughfor a complex grammar implementing the Java language specification, a large constant performance impact was incurred per input character for thepikaparser, which allowed Parboiled2 and ANTLR4 to perform significantly better than thepikaparser for this grammar (in spite of ANTLR4’s parsing time scaling between quadratically and cubically in the length of the input with the Java grammar). Therefore, if performance is important,pikaparsing is best applied to simple to moderate-sized grammars, or to very large inputs, if other parsing alternatives do not scale linearly in the length of the input. Several new insights into precedence, associativity, and left recursion are presented.
PS
If you want to know more history of BNF and REG see Guy Steele talk.
If you want to understand the terminology, like LR, LL, backtracking, etc. see this course.
If you want to learn more about dynamic programming read this.
Algorithms used in real-world applications: wikipedia article on parser generators.
Visualizing algorithms:
About ambiguity:
- The Usability of Ambiguity Detection Methods for Context-Free Grammars
- Ambiguity Detection for Context-FreeGrammars in Eli
More reading: