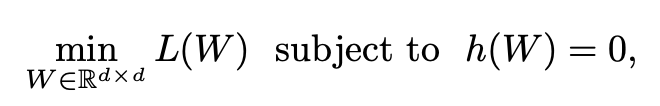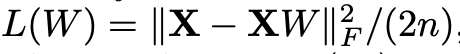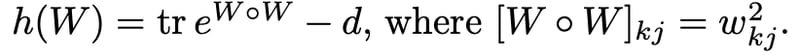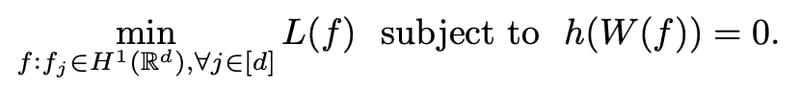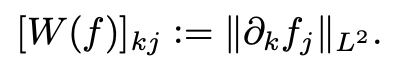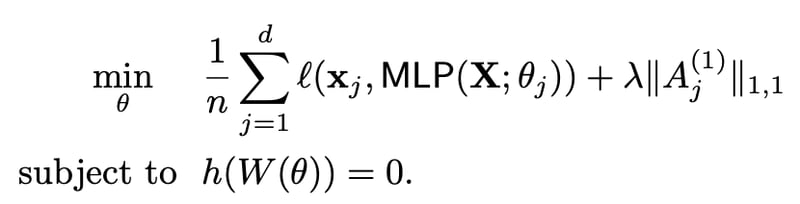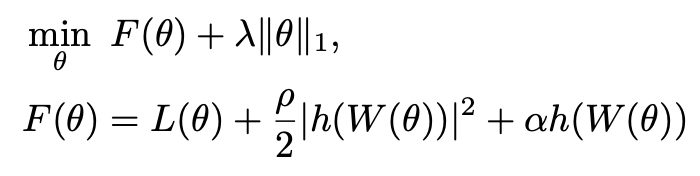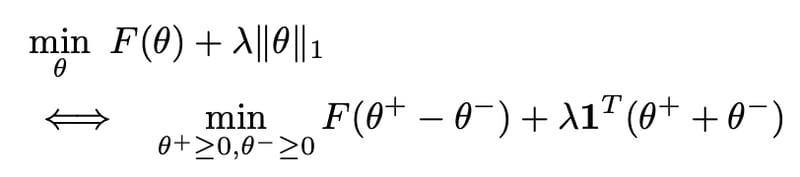選択理由

causalnexにも適用されているnotears[Zheng2018]の非線形・ノンパラメトリック版であり実用性が高そうという印象。この記事によるとcausalnexはmckinseyも注目している。なお、DAGsと複数形になっている点は注目で、因果グラフが１つとは限らないタスクを前提としている。

Paper: https://arxiv.org/abs/1909.13189
Code: https://github.com/xunzheng/notears

被引用としては[Ng2022]にて本論文の概要がまとめられている。

概要

[社会課題]先行研究である初期のnotears[Zheng2018]は因子間の関係性がパラメトリック(=母集団が確率分布で仮定できる)な線形因果モデルを仮定しているが、現実世界の因果関係は非線形のものがあり、そもそもパラメトリックであるとは限らない。
[技術課題]ノンパラメトリックであることから因果グラフの隣接行列が定義されず、非循環性の判定が困難になる。従来のアプローチでは隣接行列の指数関数のトレースから非循環性を判定していた。
[提案]解析学の見地から特定因子を関数で偏微分した値が0であることが因子が独立であることの必要十分条件であることを示し、ノンパラメトリックモデルとして定式化した。さらにその定式化が多層パーセプトロンで近似できることを示した。
[効果]先行研究[Zheng2018]を一般化し、因子間の関係が非線形かつノンパラメトリックの場合でも扱うことができる。又、一般的な最適化手法で解くことができるようになった。

線形構造方程式のパラメトリックなモデル化

[Zheng2018]で提案されている因果構造の推定は以下の最適化で定義される。

Wは隣接行列であり、因子iと因子jに因果性があれば i, j成分が１であるようなバイナリ行列である。

因子間の関係性は線形であるという仮定のため、損失関数Lは上記のように入力Xに対する二乗誤差で定義できる。

非巡回性制約は隣接行列の指数関数のトレースから表現できる。ここの部分の詳細は[Zheng2018]を参照。このブログにも解説がある。

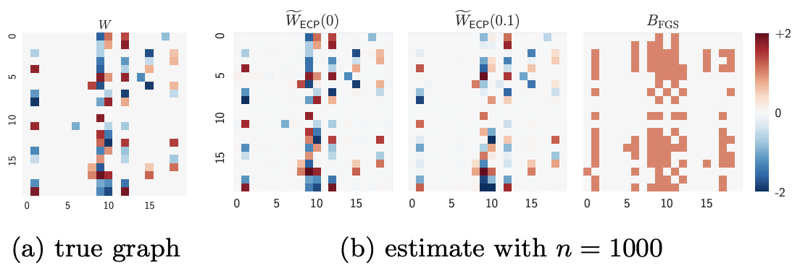
上記は[Zheng2018]での因果構造推定の実験結果である。データを生成した際の因果モデルが推定できているのがわかる。

構造方程式のノンパラメトリックなモデル化

パラメトリックな線形モデルにおいて最適化対象をL(W)と記述できるのは因果モデルの構造を識別するのに必要十分な情報を行列Wで表現できるからである。より一般的な因果モデルでは最適化対象となるのは本来、ソボレフ空間上の関数fを用いたL(f)となる。

ここで、H1はソボレフ空間を表す。ソボレフ空間上の自乗可積分函数はその微分が自乗可積分函数となることより、j番目の関数fが因子kと無関係であるには偏微分のL2ノルムが０であることが必要十分条件である。（測度論も絡んでおりあまりここに足を突っ込みたくないが、関数fの変化量に対して因子kが無摂動だったら無関係というのは何となく理解できる）ソボレフ空間についてはこの動画に丁寧な解説がある。

W(f)は上記のように偏微分のL2ノルムで定義することができる、これを用いるとノンパラメトリックな構造方程式のモデル化を行うことができる。fが線形の関数であれば線形構造方程式と同じ式になる。

ノンパラメトリック性への対処

ノンパラメトリックモデルであるL(f)の最適化は無限な次元数であるため、計算困難である。このノンパラメトリック性は様々なアプローチで解決することができ、4.1 Multilayer perceptronsもその方法の１つである。これはレイヤ数や隠れユニット数の設定により特定次元で打ち切り、パラメトリック化していることに相当する。又、これらのモデル複雑性を無限に高めることでノンパラメトリックなモデル化に近づけることができる。4.2 Basis expansionsというアプローチについても論じられているが本ブログでは省略する。
ノンパラメトリックモデルでの最適化の目的関数であるL(f)はMLPにおいては以下の式に帰着する。

関数fはMLPの場合はモデルパラメータΘであり、h層あるMLPでh個のモデルパラメータ(ベクトル)Aで表現できる。これにより、ノンパラメトリックモデルでの因子jに対するW(f)は以下に具体化される。ここで注目なのがW(f)は１層目のAで表現されている点である。

ここで目的関数L(f)は連続空間であるため、Θにおいて微分可能である。よってL(f)は以下の式になる。

ここで、ρはペナルティ制約パラメータ、αは双対変数である。上記最適化問題は制約なしL1正則化付き最適化問題であり、一般的な最適化アルゴリズムであるL-BFGS-B[Byrd1995]等を使用できる。そうすることで以下のbox-constraints formによる線形最適化となり、実装が楽になる[参照issue]。

実験

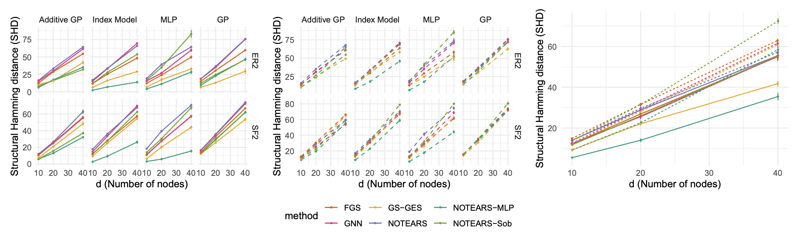
因子数(n)を変えながら各因果モデル化でSHD（Structural Hamming Distance）を計測した実験結果、左がデータ数1000,中央が200,右がそれらの平均である。GNN(Graph Neural Net)や線形のNotearsよりも今回提案しているノンパラメトリック・非線形のNotears-MLPが最もエラーが少なくなっている。

実装

causalnexはNO TEARSを採用している。_learn_structure()はオフィシャル実装と同じであるが、オフィシャル実装の方がやはり新しく損失関数の種類が増えたりしている。使用例のブログもある。