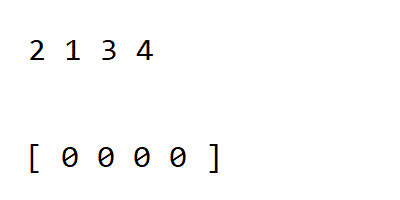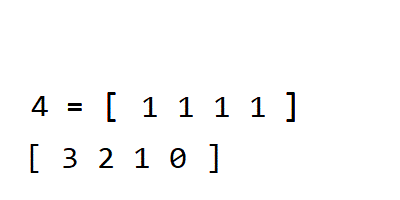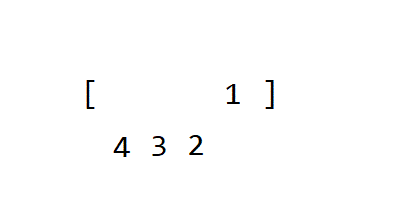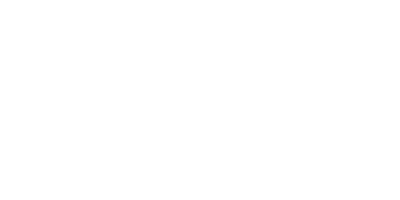Introduction
Let's continue the series of "Algorithms Every Programmer Should Know". It is the 2nd Part, in the first part, we explore the 4 Searching Algorithm. If you haven't read that please read that and here is the post.

Algorithms Every Programmer Should Know
Suraj Vishwakarma ・ Feb 15 '21
Today, we are going to look into 6 sorting algorithms that every programmer should know. So without a further ado let's get started.
Insertion Sort
Insertion sort iterates, consuming one input element each repetition and grows a sorted output list. At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list and inserts it there. It repeats until no input elements remain.
It takes one input at a time and compares it with the previous element in the list to place the selected element at the right place. For the first element, it compares with the next element. It iterated again and again until the last element of the list is put in the right place. After the last element, the list is sorted.
When to use
- When the list is small
- When the list is almost sorted only a few elements is needed to sort
Selection Sort
The algorithm divides the input list into two parts: a sorted sublist of items which is built up from left to right at the front (left) of the list and a sublist of the remaining unsorted items that occupy the rest of the list. Initially, the sorted sublist is empty and the unsorted sublist is the entire input list. The algorithm proceeds by finding the smallest (or largest, depending on sorting order) element in the unsorted sublist, exchanging (swapping) it with the leftmost unsorted element (putting it in sorted order), and moving the sublist boundaries one element to the right.
Initially, the list is divided into two-part. One sorted which is at leftmost and other unsorted lists which is at the rightmost side. Also at the start sorted list is empty and all the element is in the unsorted list. Then we pick the smallest element from the unsorted list and put it into the sorted list. Then the length of the sorted list increases and the unsorted list decreases. The process continues until the unsorted list is empty.
When to use
- To check whether the given list is already sorted or not
- When memory is small as it uses less swap
Heap Sort
Heapsort divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element from it and inserting it into the sorted region. Unlike selection sort, heapsort does not waste time with a linear-time scan of the unsorted region; rather, heap sort maintains the unsorted region in a heap data structure to more quickly find the largest element in each step.
In heap sort, the input value is stored into a heap memory with the root of the largest value from the tree. Then the largest values are stored into an array of the list. The process goes on until the heap memory is empty and the output is the sorted array.
When to use
- When the list is huge
- When to find the smallest or larger item in the list
Merge Sort
Conceptually, a merge sort works as follows:
- Divide the unsorted list into n sublists, each containing one element (a list of one element is considered sorted).
- Repeatedly merge sublists to produce new sorted sublists until there is only one sublist remaining. This will be the sorted list.
The list is divided into sublists, each list containing one element. Then each element is compared to its neighboring element and merged into another sublist according to order. This process continues to each sublist. Now each sublist has 2 elements, Now each sublist is compared to the neighbor's sublist. Each sublist having 2 elements. The list is merged into another sublist according to order. Now each sublist will have 4 elements. This process continues till there is only one sublist remaining. this sublist will be in sorted order.
When to use
- When the list is linked list
- When the list is huge
Quick Sort
Quicksort is a divide-and-conquer algorithm. It works by selecting a 'pivot' element from the array and partitioning the other elements into two sub-arrays, according to whether they are less than or greater than the pivot. For this reason, it is sometimes called partition-exchange sort.[
In quicksort, we pick an element from the list called a pivot(Mostly it is either the first or the last element of the list). Then we reorder the array in such a manner that all the elements that are less than the pivot are placed before the pivot and elements greater than pivot values are placed after the pivot value.
We repeat this step in both the sublists i.e. before and after the pivot value. This continues until the list is sorted.
When to use
- When the list is small
- It is preferred for array
Counting Sort
In computer science, counting sort is an algorithm for sorting a collection of objects according to keys that are small integers; that is, it is an integer sorting algorithm. It operates by counting the number of objects that have each distinct key value and using arithmetic on those counts to determine the positions of each key value in the output sequence.
After taking input, counting sort count number of times the element is repeated in the list. Thus having 2 distinct values one for element and the other for the count. Then doing the arithmetic calculation on it and deciding the position of each element in the list.
For arithmetic calculation, read GeeksforGeeks article on counting sort
When to use
- When the range of input values isn't greater than the number of values to be sorted.
- For a small list of array
Last Note
I hope this article helped you in learning algorithms. Thank You for reading the blog post.